Органолептический анализ имеет большое значение при оценке качества рыбных продуктов, так как это наиболее простой, дешевый и быстрый, а в ряде случаев и единственно возможный способ, позволяющий отличить высококачественный продукт от ординарного, фальсифицированный — от натурального, выявить ранние признаки порчи продукта и т.д.
Органолептическую оценку продуктов осуществляет комиссия специали-стов-дегустаторов, которая выполняет роль измерительных или контрольных приборов, поэтом)’ органолептическая оценка всегда субъективна. Однако существуют возможности повышения объективности сенсорных исследований, в частности путем обучения пшрокого круга специалистов методам дегустационных исследований, перехода на количественную оценку органолептических показателей на основе применения балльных шкал.
Особенно важно преодолеть у некоторых специалистов предубеждение к органолептическим методам анализа, так как даже в случае перехода на инструментальные методы оценки качества продукта органолептическая оценка останется «посредником» между приборами и чувственным восприятием свойств продукции потребителем.
Методы органолептической оценки качества рыбной продукции благодаря их простоте и оперативности широко используются при оценке сырья и готовой продукции, при выполнении задач, связанных с улучшением качества продукции, обеспечивают получение важной информации при разработке новых продуктов. Благодаря развитию методического обеспечения и использованию его в научной и практической деятельности технологов и товароведов рыбных продуктов за последнее время повысился профессиональный уровень органолептиков: развиваются описание и трактовка терминологии, происходит ее унификация, разрабатываются и применяются балльные шкалы, что обеспечивает квалиметри-ческий подход к оценке органолептических показателей. Широко используется такой сложный метод, как профильный анализ.
Оценку качества производственных партий рыбной продукции по органолептическим и физико-химическим показателям проводят строго в соответствии с действующими государственными стандартами (ГОСТ) или нормативной документацией, отражающей требования к номенклатуре показателей и содержащей методики испытаний.
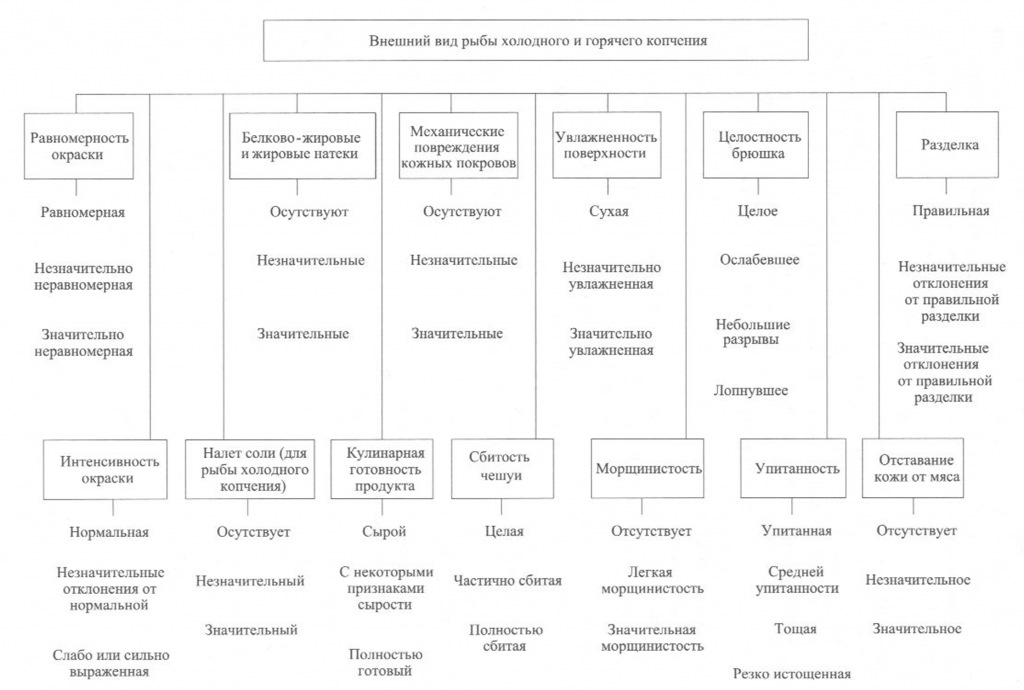
Основными органолептическими показателями качества рыбы холодного и горячего копчения являются: внешний вид, консистенция, вкус и запах [Сафронова, 1998].
Определение внешнего вида. Внешний вид копченой рыбы оценивают по признакам, приведенным на рис. 38.
При внешнем осмотре копченой рыбы оценивают равномерность и интенсивность ее окраски. Равномерность окраски характеризуется по наличию светлых пятен, возникающих из-за неполной обработки поверхности дымом, ожогов кожи, отпечатков прутков и загрязнения сажей. Нормальной по интенсивности считается окраска от светло-золотистой до темно-золотистой с серебристым отливом, но цвет может быть и темным в зависимости от естественной окраски кожи рыбы.
Внешний вид копченой рыбы оценивают также по наличию белковожировых натеков в виде отдельных пятен, узких полос различной площади. Этот признак в зависимости от степени натека характеризуют как значительный или незначительный.
На поверхности в различных частях тела рыбы холодного копчения может выступить избыток соли в виде белого налета (на голове, жаберных крышках, у хвостового плавника).
К механическим повреждениям копченой рыбы относятся повреждения жаберных крышек и плавников, проколы, небольшие срывы и порезы кожи, трещины на срезах и в брюшной полости, отломанные или надломанные головы, вырезы ранений.
О внешнем виде копченой рыбы судят также по упитанности, сбитос-ти чешуи, морщинистости кожи, отставанию ее от мяса, влажности поверхности, целостности брюшка, правильности разделки.
Брюшко рыбы, выкопченной в неразделанном виде, может быть целым, ослабевшим, имеющим трещины, лопнувшим. Целым считается брюшко плотное, без повреждений ткани. В лопнувшем брюшке бывает нарушена целостность брюшных стенок, возможно выпадение внутренностей.
По внешнему виду судят о кулинарной готовности рыбы горячего копчения. В готовом продукте полностью свернувшаяся кровь, мясо, икра или молоки проварены, без признаков сырости, мясо легко отделяется от позвоночника.
Определение запаха. Запах копченой рыбы исследуют, пронюхивая ее поверхность или мясо на поперечном разрезе, сделанном ножом с тонким лезвием в средней, наиболее мясистой части тела рыбы, или прокалывая тело рыбы в нескольких местах и пронюхивая с помощью деревянной шпильки (заостренной конусообразной палочки из сухого, мягкого, непахучего дерева). Диаметр шпильки в средней части должен быть не более 0,6 см. После каждой пробы шпильку необходимо тщательно очищать, а после исследования каждого дефектного экземпляра рыбы шпильку следует заменять новой.
Запах копченой рыбы оценивают, руководствуясь схемой, приведенной на рис. 39, по степени выраженности аромата, свойственного данному вид)’ рыбы и типичного для данного способа обработки (наличию весьма своеобразного и гармоничного букета, характерного для копченой рыбы), а также по присутствию запаха окислившегося жира.
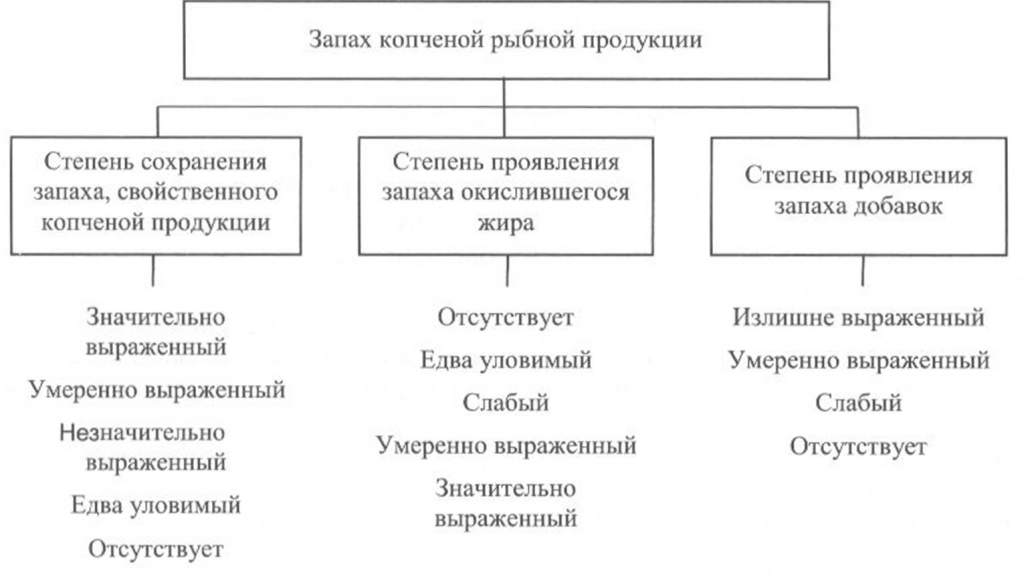
При исследовании запаха копченой рыбы, приготовленной с использованием различных добавок, определяют также степень проявления запаха соответствующих добавок.
Определение вкуса. Вкус копченой рыбной продукции оценивают, руководствуясь схемой, приведенной на рис. 40.
Вкус копченой рыбы определяют при непосредственном опробовании тонких ломтиков образцов продукта путем тщательного их разжевывания.
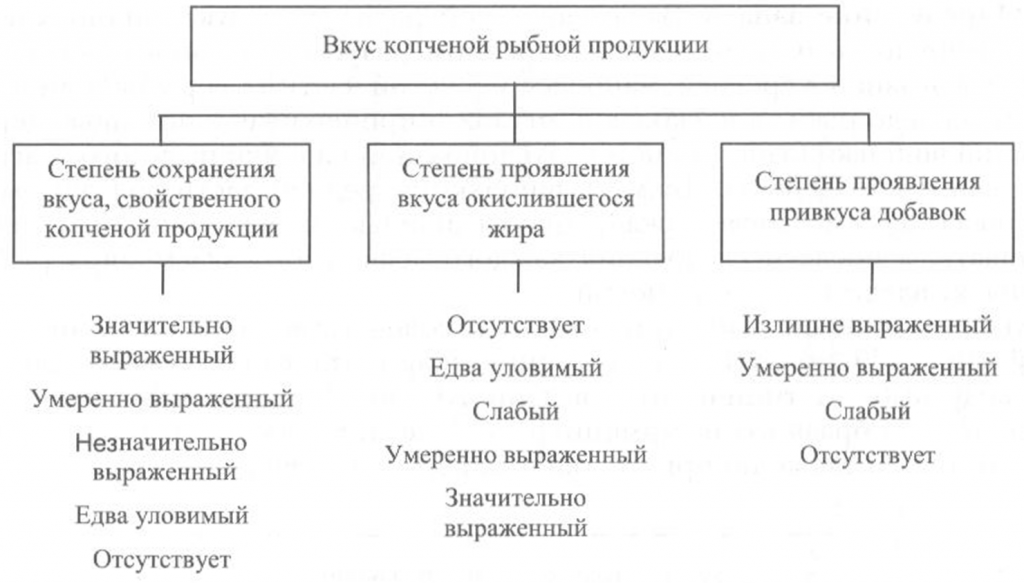
Образец для опробования вырезают острым ножом из средней, наиболее мясистой части тушки рыбы перпендикулярно хребтовой кости. Толщина вырезанных ломтиков должна быть не более 1 см, а температура образцов — около 20 °С.
Вкус копченой рыбы оценивают по степени его выраженности, соответствующему данному виду сырья и данному способу обработки, наличию характерного специфического вкуса копчености и привкуса окислившегося жира.
При исследовании вкуса копченой рыбы, приготовленной с использованием различных добавок, определяют также степень проявления привкуса соответствующих добавок.
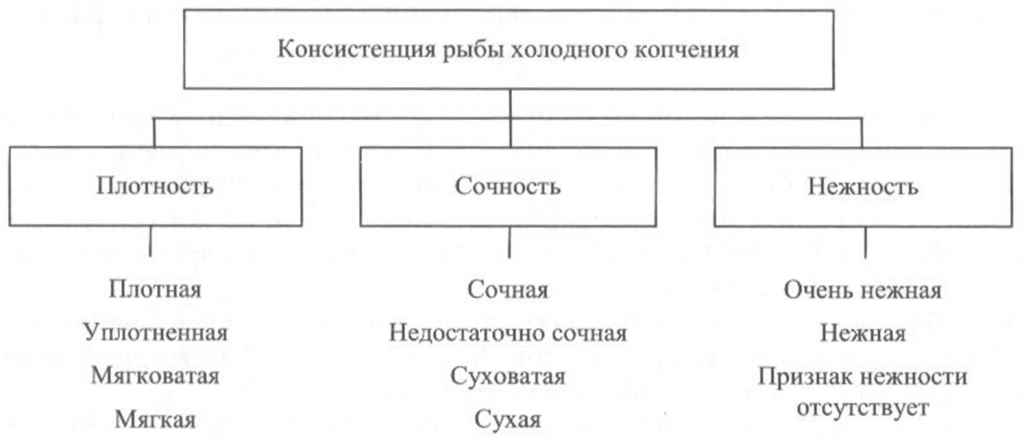
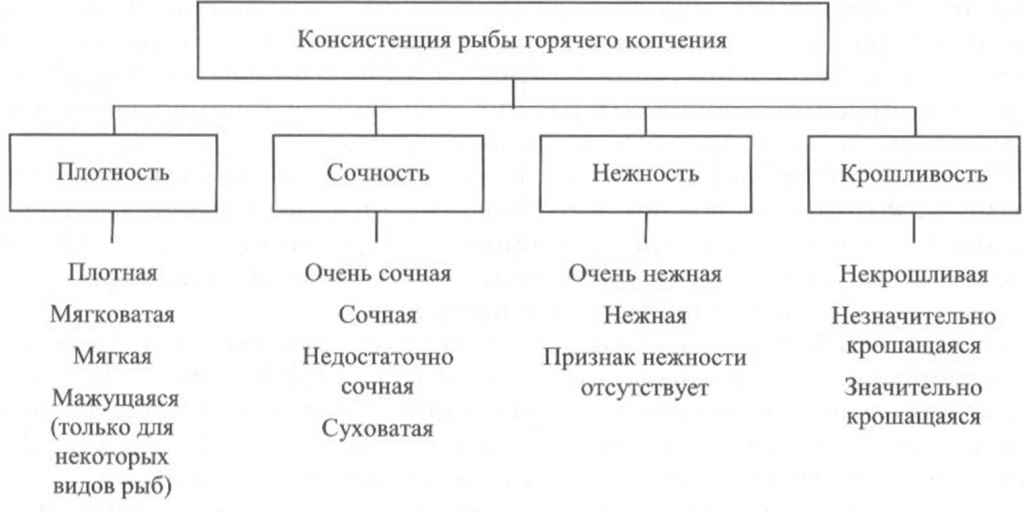
Определение консистенции. Консистенция рыбы холодного и горячего копчения характеризуется такими признаками, как плотность, сочность и нежность (рис. 41, 42). Для рыбы горячего копчения определяют еще и такой показатель, как крошливость.
Плотность оценивают прощупыванием целой рыбы пальцами вдоль спинки, надавливанием на мясо на поперечном срезе, проходящем через наиболее мясистую часть тела рыбы, разжевыванием ломтиков спинной мышцы, взятой в области поперечного среза. При исследовании рыбы, выкопченной в виде кусков, надавливание проводят в наиболее мясистых участках и по торцам куска.
Для определения сочности рыбу разжевывают и при этом сосредотачивают внимание на легкости отделения тканевого сока и его количестве, а также на степени смачивания им ротовой полости.
холодного копчения
Для оценки нежности кусочки рыбы не разжевывают, а сдавливают пробу между языком и передней частью неба. При определении нежности акцентируют внимание на способности ткани легко превращаться в однородную массу, пригодную к проглатыванию, не вызывающую при этом механического раздражения полости рта.
горячего копчения
Для определения крошливости крупную рыбу горячего копчения разрезают в поперечном направлении острым ножом, а мелкую разламывают в средней части тела [Сафронова, 1998].
Контроль за органолептическими показателями качества копченой рыбы осуществляет изготовитель в каждой партии выпускаемой продукции.


Свежие комментарии